Jleeoslo

Jleeoslo

This is my playground for data exploration and experimentation

[Decision Tree] Understanding Decision Trees and their recursive algorithms

4 minute read

Decision Tree

  • A Decision Tree is a tree-structured in which each internal node represents a criterion on an attribute , each branch represents the outcome of the criterion, and each leaf node represents the final target values(class labels or estimated numbers).

  • The following shows how certain data can be turn into a Decision Tree for classification.

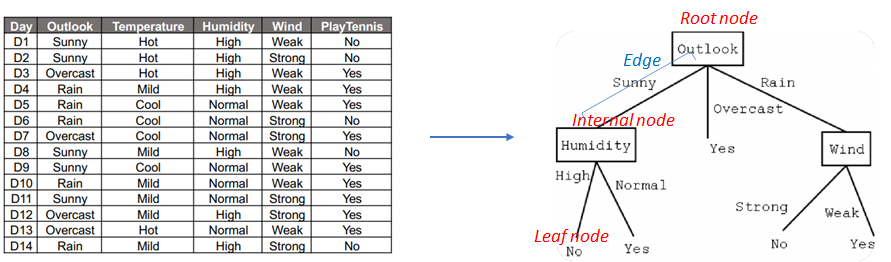
    source: fastcampus


  • Pros and Cons of Decision Tree

    • Pros: (1) Most of all, Decision Trees are simple to understand and interpret. (2) Decision trees help to determine worst, best and expected values for different scenarios. (3) Decision trees don’t require statistical assumptions (cf. LDA).

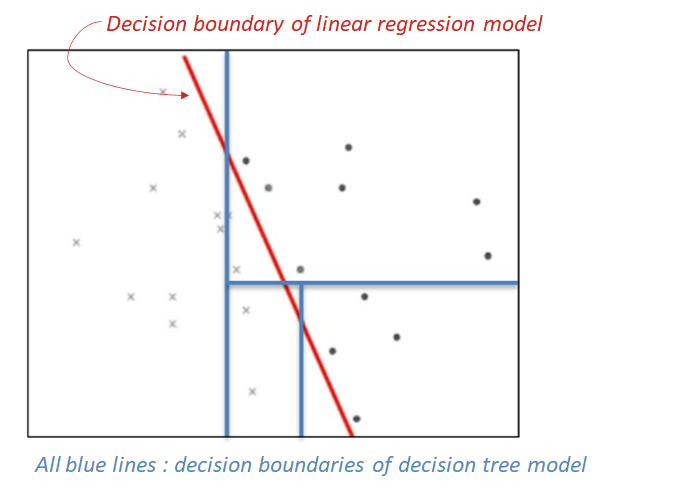
    • Cons: (1) Decision Trees are unstable; a small change in the data can lead to a large change in the structure of the optimal decision tree. Then, the domain gap between training data and test data should be small for good performance. (2) Decision Trees are often relatively inaccurate. There are alternative models such as Random Forest to alleviate this problem. (3) Calculations can get complex. For instance, in the figure below, one decision boundary of linear regression is better at classifying dataset than the Decision Tree with three nodes.

source: 세종대*최유경 교수 9주차 의사결정나무 Part1(유튜브 강의)


  • Decision trees can be applied to classification and regression problems.


Classification Tree

  • Decision trees where the target variable can take class labels are called classification tree.

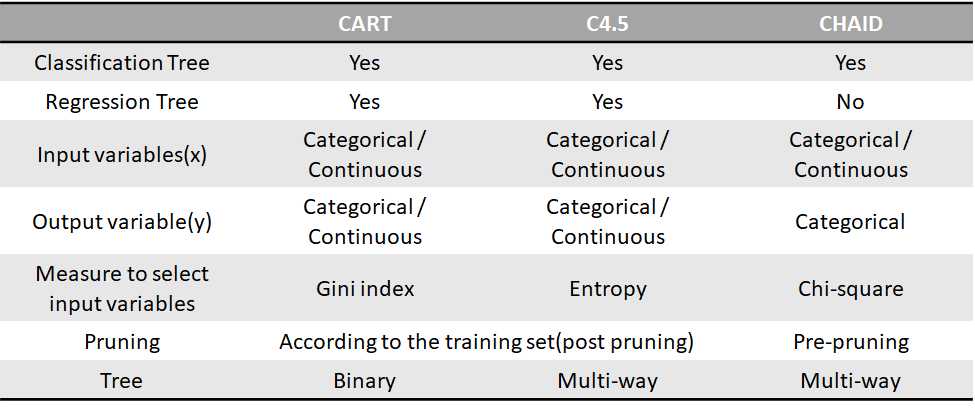
  • For classification problems, recursive partitioning algorithms such as CART(Classification And Regression Tree), C4.5, C5.0, CHAID(Chi-Square Automatic Interaction Detection) can be applied. The table below summarizes the details.


  • CART (Classification & Regression Tree)

    • CART can be used for both classification and regression problems.
    • CART only uses binary splits, meaning that each parent node always has two child nodes.
    • When it comes to pruning, CART generates a tree with training data and exercises pruning with test data.
    • CART uses Gini index as measure of selecting input variables(attributes). The following example describes how input variables(gender, marital status) are selected or not as a node by calculating Gini index.
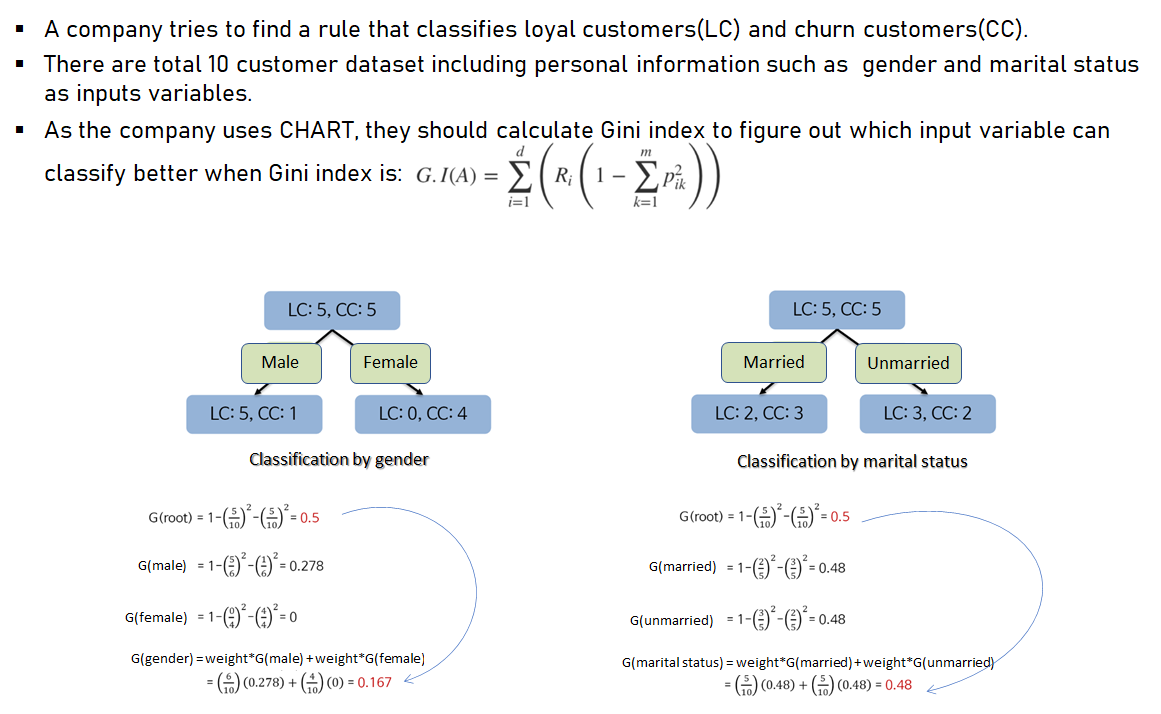
  • When gender is selected as a node, Gini index decreases larger. Therefore, gender should be the criterion of the classification in this example.
source: 세종대*최유경 교수 9주차 의사결정나무 Part2(유튜브 강의)


  • C4.5

    • C4.5 can be used for both classification and regression problems.
    • C4.5 uses multiple splits.
    • C4.5 generates a tree and exercises pruning with training data.
    • C4.5 uses Information Gain(IG) as measure of selecting input variables(attributes). The following example describes how input variables(gender, marital status) are selected or not as a node by calculating IG.
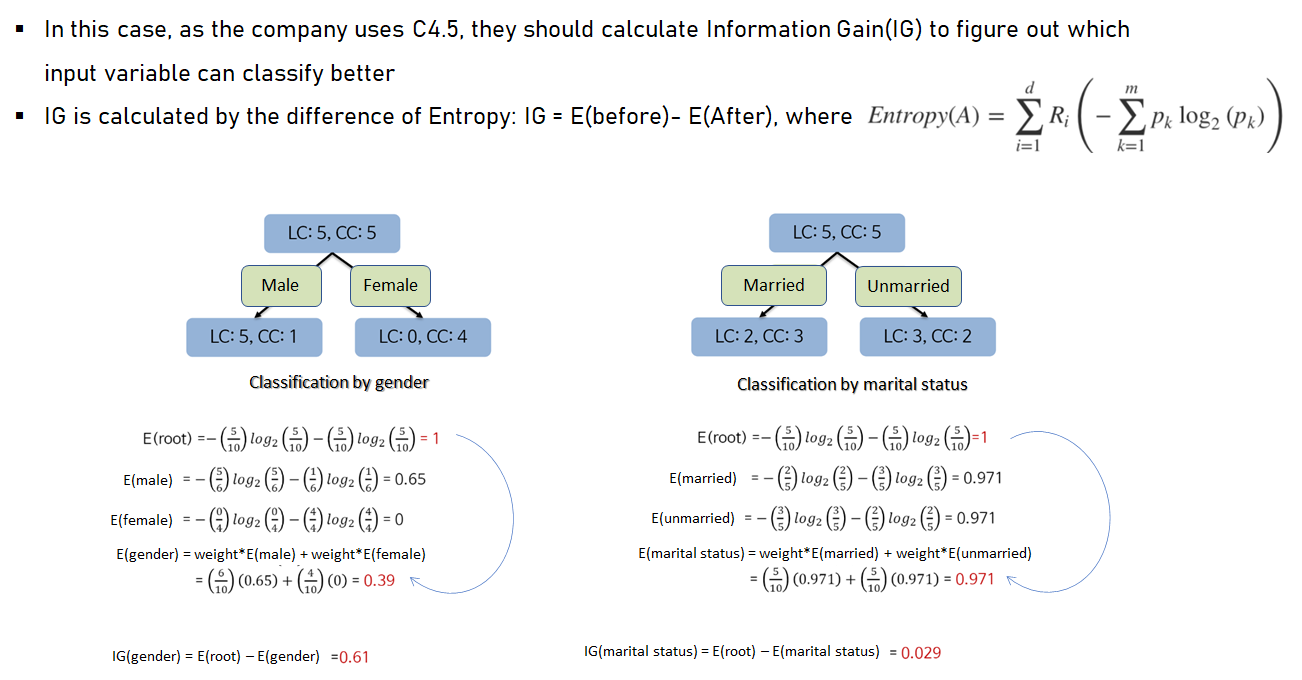
    • When gender is selected as a node, IG is larger. Therefore, gender should be the criterion of the classification in this example.
    source: 세종대*최유경 교수 9주차 의사결정나무 Part2(유튜브 강의)


  • In the example above, IG is used for binary slits. When it comes to multiway splits, C4.5 can use information gain ratio(IGR) to reduce a bias towards multi-valued attributes by taking the number and size of branches into account when choosing an attribute. IGR(A) is calculated by dividing IG(A) by IV(A) where IV(A) refers to intrinsic value of A having following formula.
6


  • Overfitting problem in decision tree

    • Overfitting occurs when a learning algorithm continues to develop hypotheses that reduce training set error at the cost of an increased test set error. In other words, the algorithm is too dependent on that training set and it is likely to have a higher error rate on new unseen data.

    • To avoid overfitting in decision tree, one can design stop condition and apply pruning. In the former case, by designating specific parameters for the depth of the tree or for the minimum number of observations of a node, we can stop a tree from keeping growing. In CHAID, instead of pruning, stop condition is used. When the decrease in the p-value of the chi-square statistic is minimal, the tree stops growing.

      In contrast, pruning is reducing the size of the tree after growing the full tree. By removing(merging) sections of the tree that are non-critical and redundant to classify instances, overfitting is reduced, hence, predictive accuracy is also improved.


Regression Tree

  • Decision trees where the target variable can take continuous values are called regression tree.
  • When input variables enter, the output value is estimated by calculating the mean of data within the corresponding leaf node.
  • Splits are chosen to minimize the the sum of the squared errors between the observation and the mean in each node.
  • Furthermore, the performance of regression tress can be measure through RMSE(root mean squared error). We can select the optimal model with the smallest RMSE.


More to read

Reference

Updated:

You may also enjoy