[Naïve Bayes] Understanding mathematical concepts of Naïve Bayes classifiers with an example

2 minute read

Understanding Naïve Bayes classifiers

Naïve Bayes are a set of supervised learning classification algorithms. Naïve Bayes predict labels of the class ‘y’ according to the conditions of features x₁,x₂, … ,x_n.
Naïve Bayes are based on applying Bayes’ theorem with strong conditional independence assumptions between every pair of features given the labels of the class.
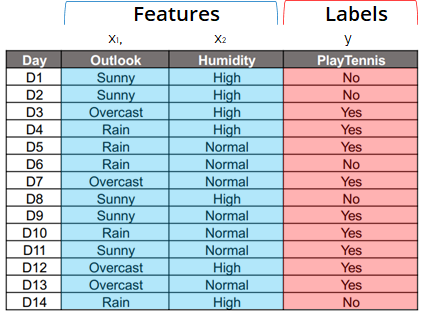
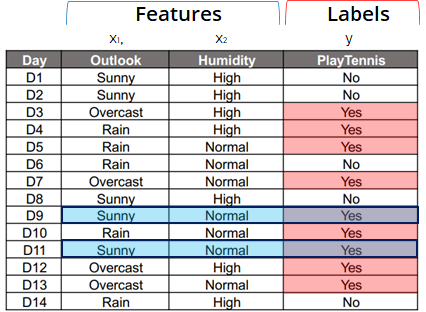
source: fastcampus.co.kr
- When fitting a Naïve Bayes classifier on the example data above, a label(yes or no) of playing tennis can be predicted depending on the conditions of features (outlook and humidity).
- Following Bayes’ theorem, the two features ‘outlook’ and ‘humidity’ are considered to be independent(although in real life they are related).

Bayes’ theorem is stated as the following equation when A and B are events and P(B) ≠0.

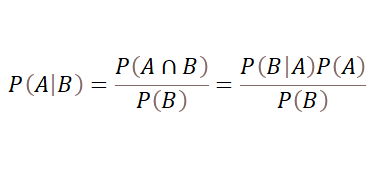
Furthermore, When A₁, … , A_k are a set of mutually exclusive events with prior probabilities P(A_i) (i = 1, …, k) , For any other event B for which P(B) > 0, the posterior probability of A_i given that B has occurred is:

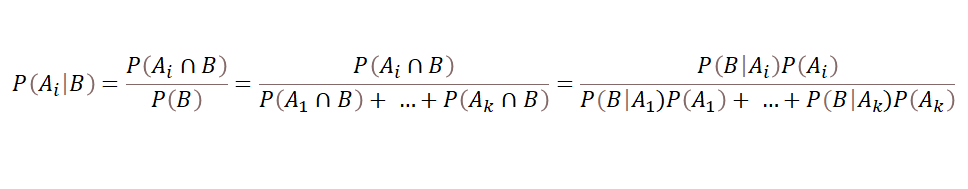
By applying Bayes’ theorem, the formula of Naïve Bayes is:

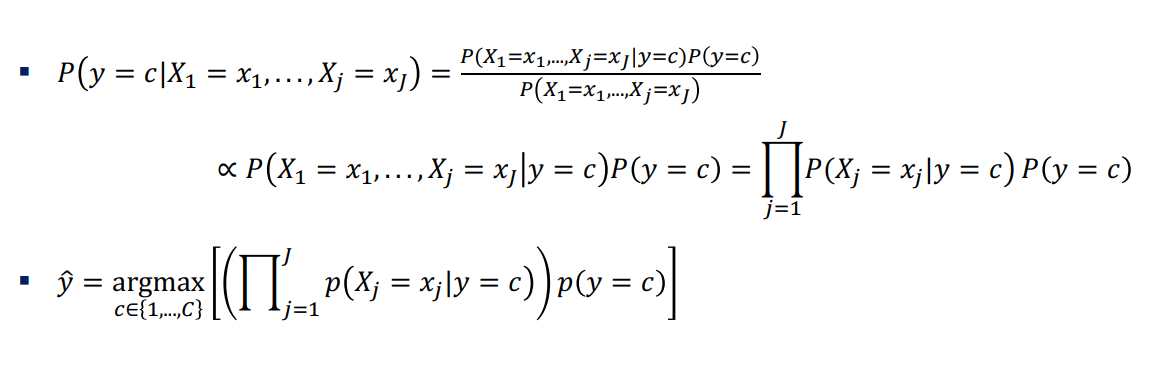
Then, in the same example, the label of playing tennis when outlook is sunny and humidity is normal can be decided like this:

According to the argmax function, between Yes and No, the one with the higher probability will be labeled.

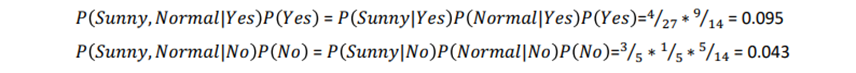
Therefore,

source: fastcampus.co.kr

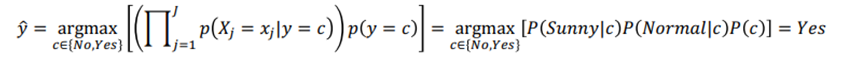
Regardless of the number of features, Naïve Bayes classifier calculates the final probability is by the product of each probability, so the calculation process is simple and convenient.
Yet, as Naïve Bayes classifier assumes conditional independence between features, the association between features cannot be explained in actual data. As already mentioned, in the example data ‘outlook’ and ‘humidity’ are considered to be independent although in real life they are related.

Gaussian NB : when features are numerical
- From the formula of Naïve Bayes, it’s calculation follows:
- It is assuming that a feature follows a Gaussian normal distribution. In other words, when a label is set as ‘c’, the certain feature ‘x’ follows a normal distribution and its mean and variance are calculated within the sample which are labeled as ‘c’.
Multinomial NB : When features are discrete.
- From the formula of Naïve Bayes, it’s calculation follows:
Bernoulli NB : When features are discrete and binary.
- From the formula of Naïve Bayes, it’s calculation follows: