회귀분석 (regression analysis)

회귀분석 (regression analysis)

회귀분석은 입력 변수(들)와 목표 변수 간의 인과관계를 파악하기 위해 사용된다.

회귀분석은 로지스틱 회귀분석, 조절효과, 매개효과, 구조방정식을 알기위해 가장 먼저 공부해야할 개념이다.

회귀분석이란?

• 독립변수와 종속변수가 모두 연속형 변수(등간척도, 비율척도)일 때 사용하는 분석방법
• 추정방식은 OLS(Ordinary least square)로 이루어지는데, 이는 오차의 제곱을 최소화 하는 직선이라는 의미이다.

회귀분석의 원리

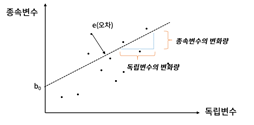
• 회귀식: y = b₀ + b₁ · x + e

  이때, y: 종속변수, x:독립변수, b₀ : 기울기(즉, 종속변수의 변화량 / 독립변수의 변화량), e: 오차

(출처: 패스트캠퍼스)

• 편차들의 제곱을 최소화 할 수 있는 직선이 이 점들을 대표할수 있다.

• 가장 중요한 것은 기울기. 즉, b₁ 이 ‘0’인가 아닌가가 중요하다.

대표가설

• H0 : 독립변수가 종속변수에 미치는 영향의 크기는 ‘0’이다.

• H1(양측검증): 독립변수가 종속변수에 미치는 영향의 크기는 ‘0’이 아니다.
• H1(단측검증): 독립변수가 종속변수에 미치는 영향의 크기는 ‘0’보다 크다.

회귀분석의 특징

• 회귀분석에서는 여러 개의 독립변수를 포함하는 것(다중회귀분석)이 가능하다. 예를 들어 독립변수가 4개라고 가정할 때, 회귀식은 y = b₀ + b₁·x₁ + b₂·x₂ + b₃·x₃ + b₄·x₄

• 여러 개의 독립변수들을 포함하는 경우, 독립변수들이 서로 함께 영향을 미치는 교집합은 제외되고, 각자의 독자적인 영향력으로 계산되어진다.

설명량(R²)

• R²가 증가할 수록 회귀식에 설명되어지지 못하는 오차는 감소한다. 즉, 표본으로 추정된 회귀선이 관찰치를 얼마나 적절히 설명하는 가를 나타내는 척도이다.
• R²의 증가량을 이용해서 독립변수의 포함여부를 결정한다. 예를 들어, y₁ = b₀ + b₁·x₁ + b₂·x₂ + b₃·x₃과 새로운 독립변수x₄를 하나 더 추가시킨 y₂ = b₀ + b₁·x₁ + b₂·x₂ + b₃·x₃ + b₄·x₄이 있을 때, R²의 증가량이 0이 아닐 경우 x₄를 포함할 수 있으나 반대로 0이거나 0과 비슷할 경우 설명력이 증가하지 않음으로, 굳이 x₄를 포함시키지 않는다.

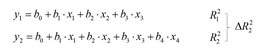
출처: 패스트캠퍼스

More to read

• R 기초 통계 / 회귀 분석이란? (https://ybeaning.tistory.com/19)]( More to read R 기초 통계 / 회귀 분석이란? (상관분석, 설명력, 다중공선성) https://ybeaning.tistory.com/19) )
• Logistic Regression Analysis 로지스틱 회귀분석 (https://m.blog.naver.com/libido1014/120122772781)
• [SPSS 26] 로지스틱 회귀분석(Logistic Regression) – 동시입력(https://m.blog.naver.com/y4769/221851780608)

Reference

• 패스트 캠퍼스 데이터 분석 입문 올인원 패키지 강의